Computed tomography
Generally defined as a process during which the inner characteristics of an object can be determined through systematic observations of it. The corresponding mathematical process was developed by the Austrian mathematician Johann Radion. Due to how widespread it is and its increasing significance for the testing of castings, x-raycomputed tomography is usually associated with the term computed tomography, although other tomographic processes (e.g. ultrasound tomography) are possible.
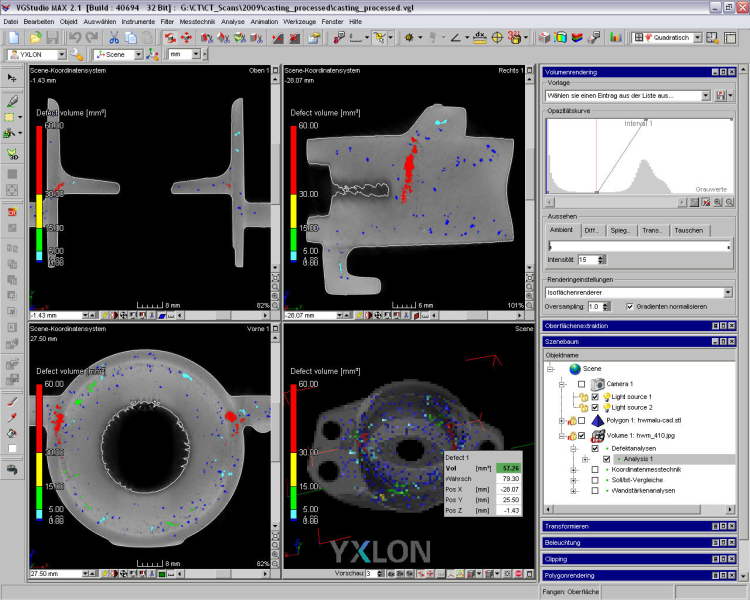
In x-raycomputed tomography, a large number of radioscopic recordings (radioscopy) of the sample are used to create a three-dimensional model of the sample volume which is investigated. Here, the value of each point in the model ideally corresponds to the linear x-ray absorption coefficient on the corresponding place in the sample. This x-ray absorption coefficient is largely dependent on the density of the material, meaning that in initial approximations we can often speak of a sample density image. Through this, computed tomography can give an insight into the inner structure of a component which is free from overlap, whereby it is possible to recognize inclusions, cavities, porosity or a multi-phase object structure. In addition, outer but also inner geometry can be measured.
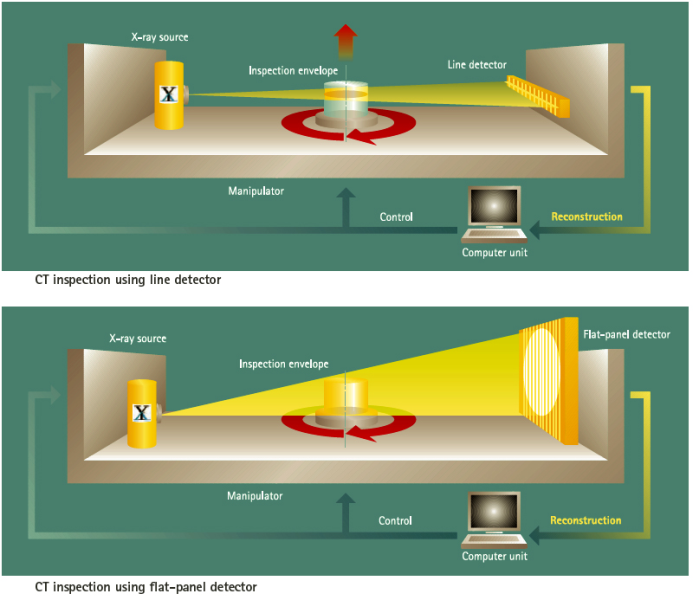
In industrial (not medical) computed tomography, a sample is usually rotated around its own axis under x-ray. At the same time, x-ray images are taken of the test object from various angles. The number of projections which are recorded depends on the number of data points to be reconstructed in the volume; in normal cases this is several hundred recordings. A distinction is often made between the recordings systems of 3D computed tomography, which is most widespread in the testing of castings today, and 2D computed tomography. In the reconstruction, a voxel data set can be calculated from the individual radiographic recordings. This can subsequently be visualized in 2D and 3D. Figs. 1 - 4 (YXLON International GmbH) shows application examples.
In computed tomography, the ideal sample geometry is a cylinder which has the same maximum material thickness in all directions subjected to radiation. This avoids a loss of information during the recording due to an over-saturation of the detector on thin areas of material and/or insufficient penetration in thick sections of the material. In contrast to this, a panel shape is an unsuitable sample geometry as, in one extreme, only the thickness of the panel and, in the other extreme, only the width of the panel must be subjected to radiation.
The resolution which can be achieved in computed tomography largely depends on the size of the sample, the power (focus, energy, radiation intensity) of the x-ray tubes and the composition of the sample. The recording times in computed tomography vary depending on the use and requirements for the measurement between < 1 minute and several hours.
A new development is the InlineCT, which includes the methods of the fast computed tomography for mass production.