Continuity equation
In the field of foundry technology, the term continuity equation refers to the balance equation for a volume subject to a stationary pipe flow (e.g. melt flowing into a downsprue).
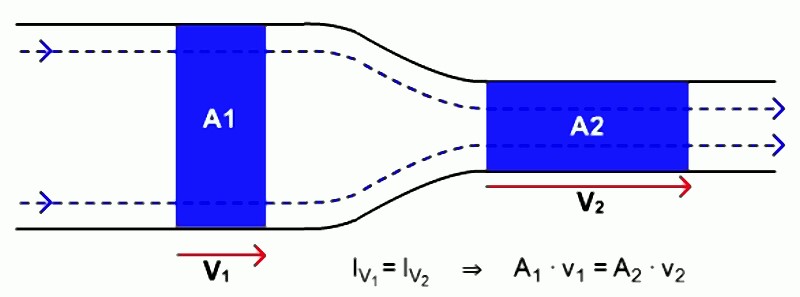
The flow volume in a pipe of variable diameter (Fig. 1) is constant if the pipe is passed by an incompressible fluid (water, liquid metal). If the diameter decreases, the flow rate must increase, and vice versa. Therefore, the continuity equation for incompressible liquids according to eq. 1 applies:
Eq. 1:
In case of gases, the balance is established for masses instead of volumes. Since the pipe now has capacity for the mass parameter as a result of gas compression, the continuity equation only applies to stationary flows according to eq. 2:
Eq. 2:
Derivation of the continuity equation
The continuity equation is based on the principle of the conservation of mass. It states those conditions under which the mass of a liquid or gas flow remains constant in a certain volume. In order to calculate the change in the flow rate of liquid particles passing through a variable cross section, it is therefore assumed that the flow is laminar and that the compressibility κ is zero.
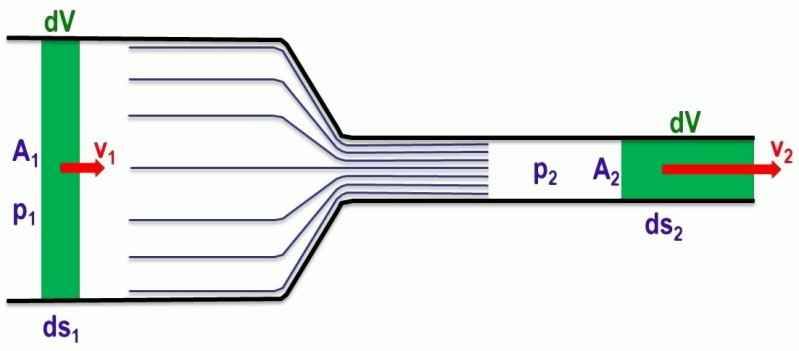
Now, a liquid flowing through a narrowing pipe is considered, as shown in Fig. 2. The following applies to a volume element dV of this liquid according to eq. 3:
Eq. 3:
At a constant density ρ, the mass dM contained in this volume element then is (eq. 4):
Eq. 4:
Then, according to eq. 5, the following mass flows through the surface area A1 in the time dt:
Eq. 5:
dV1 = A1 · ds1 gives eq. 6:
Eq. 6:
The conservation of mass implies that the same mass per time must also flow through the smaller surface area A2, resulting in eq. 7:
Eq. 7:
Under the condition that density is constant, i.e. compressibility κ = 0, and with vi = ds1/dt, this results in the known continuity equation:
Eq. 8:
Therefore, the cross-sectional area is inversely proportional to the flow rate.
The reason for the increase in flow rate is the pressure difference Δp = p2 - p1.
Additional references:
Gate system
Casting method
Nominal volume flow