Downsprue
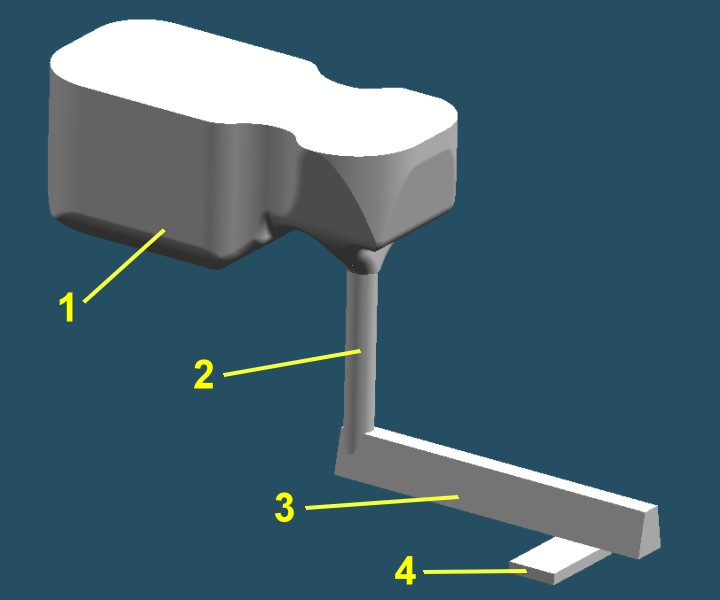
First part of the downsprue system, constisting of the following components which are also shown in Fig. 1:
- 1) Sprue cup or pouring basin
- 2) Sprue channel
- 3) Runner (also called slag runner, distributor)
- 4) Gate
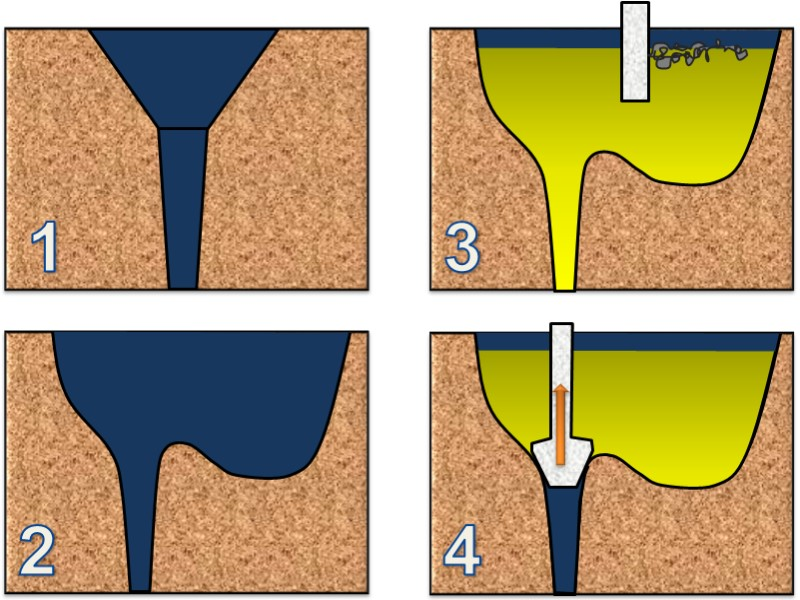
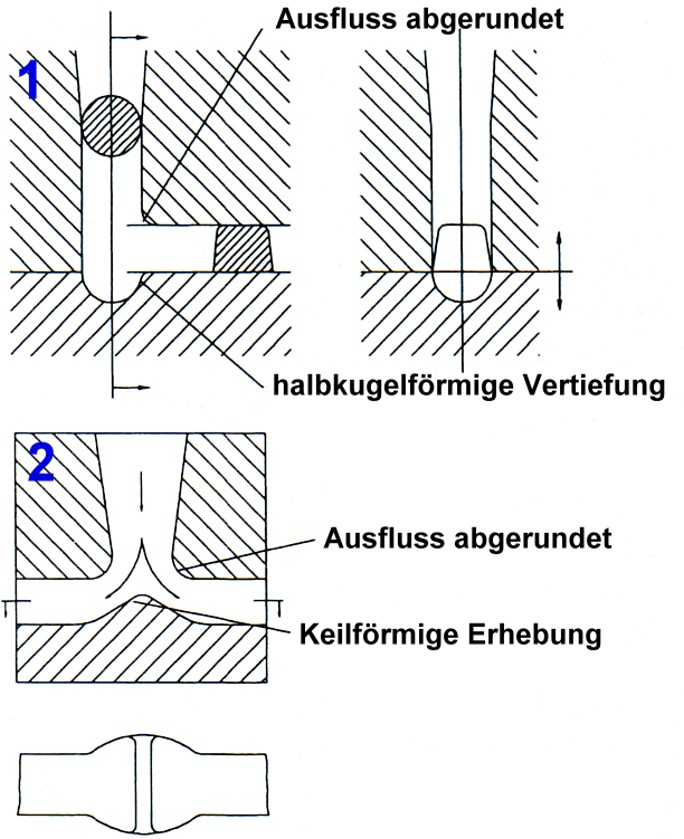
Metal from the ladle is filled into the downsprue. The latter is either designed as a cup with a circular or rectangular cross section (Fig. 2, 1) or as a basin in the shape of a pear cut in half (Fig. 2, 2 to 4). In contrast to the cup-shaped downsprue, a pouring basin has the advantage that the inlet and outlet points are spatially separated. This means that the metal settles more quickly upon pouring and that slag, foam and air are not purged into the mold due to suction from the sprue channel: all this depends on the basic requirement that the basin is appropriately sized and designed and that it can be kept full at the given pouring volume of the ladle. Another way to hold back contaminants, dross and slag in the downsprue is to integrate a slag skimmer into the pouring basin (Fig. 2, 3).
Large castings require specifically sized basins. Here, the outlet into the ingate is usually closed with a plug and is only opened once the basin has been filled completely (Fig. 2, 4). In order to avoid flow interruptions, the junction between the bottom of the basin and the ingate should be sufficiently rounded.
The sprue channel can also be called sprue passage or inlet channel and connects the pouring basin or sprue cup to the runner. The sprue channel’s task is to vertically feed the melt into the runner. Sprue channels for sand molds usually have circular cross sections. For gravity dies with a vertical partition plane, the cross section of the sprue cup is often rectangular and tapered, creating a trapezoidal cross section.
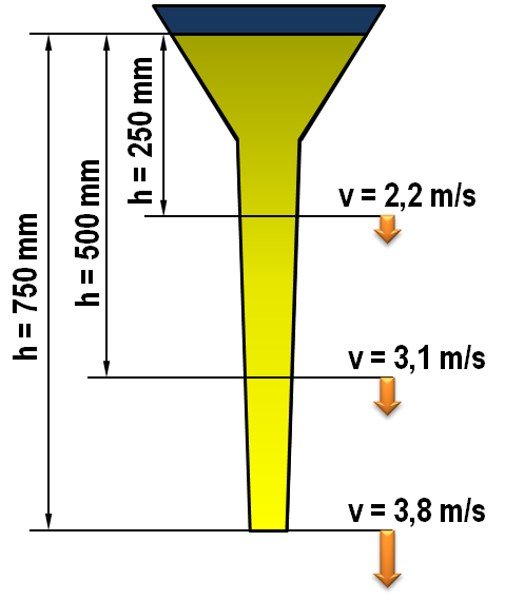
Theoretically, the flow rate of metal flowing in a vertical sprue channel reaches the values indicated in Fig. 3 due to the effect of gravitation. In the ideal case, if there is neither friction nor counterpressure, the flow rate is as follows according to eq. 1:
Eq. 1:
v = flow rate in the vertical sprue channel in m/s; g = gravitational acceleration, 9.81 m/s² ; h = effective head in m
Accordingly, the volume flow and pouring rate are primarily determined by the flow rate and flow areas. However, the pouring channel is subject to friction losses which rise with an increasing flow area. As the metal level increases, the metallostatic counterpressure in the mold cavity also rises, reducing the effective head of the downsprue.
The sprue channel leading vertically downwards should appropriately be tapered, not only for mold-related reasons but also considering the fact that the falling metal jet becomes narrower as the fall velocity increases. If the sprue channel is perfectly cylindrical, the narrowing area of the metal jet would cause air to be drawn in, resulting in turbulences and foaming.
Based on his studies and calculations, Friedrich Nielsen was able to prove that the sprue channel is not a part of the liquid vessel as suggested by Torricelli. He found that the flow rate of the liquid, i.e. the molten metal, cannot be continuously greater at any point of the inlet than is defined by the static pressure head at this particular point. This means that, if the inlet has a constant cross-sectional area from top to bottom, it is impossible for a compact flow to form. Even a slight taper would not change this fact.
Therefore, only such an amount of metal per unit of time can flow into the upper end of the inlet as is permitted by the static pressure and cross-sectional area at this point. Although the flow rate increases under the law of free fall (according to eq. 1) as the metal continues to fall, the flowing melt quantity does not. As a consequence, the metal flow contracts or is split into multiple flows at a high head. As long as the sprue cup is not completely filled with melt, air can be entrained and mixed with the melt, as can be seen in the schematic representation in Fig. 4.
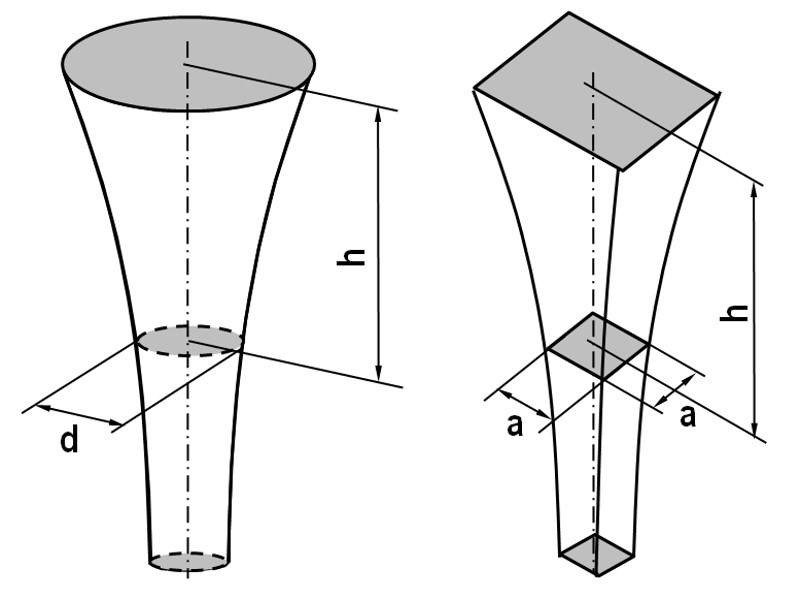
The narrowing of the cross-sectional area can be calculated on the basis of the physical law of free fall and used to define the channel areas for the downsprue. According to this, the channel diameter d for a certain head h according to eq. 2 (Fig. 5) is:
Eq. 2:
d = sprue channel diameter in cm; V = flow volume in cm³/s; h = head in cmWhen choosing a square downsprue area instead of a circular one, with the dimensions a · a (Fig. 5), this yields, by analogy, eq. 3:
Eq. 3:
These downsprues are very similar to the Nielsen downsprues (see below). The liquid metal reaches a considerable flow rate the lower end of the downsprue, the narrowest cross section. Due to the 90° deflection from the end of the downsprue to the runner, the cross-sectional area of which usually being greater than the smallest downsprue area, the flow rate is significantly reduced, i.e. the flow is slowed down. At this point, the risk of turbulent flows forming and causing particles to be washed out of the mold and casting gases to be entrained is particularly high. Fig. 6 illustrates two examples of junctions designed with favorable fluidic properties.
Nielsen downsprue for sand and gravity die castingFriedrich Nielsen has modified eq. 1 using the continuity equation (eq. 4), wherein the flow volume is the product of cross-sectional area and flow rate, to obtain:
Eq. 4:This eq. 4 is solved for A based on eq. 1, resulting in eq. 5:
Eq. 5:
V = flow volume in cm³/s; A = cross-sectional area in cm²; v = flow rate in cm/s; g = gravitational acceleration, 9.81 cm/s²; h = head in cmFriedrich Nielsen used this equation to derive standardized inlets for sand and gravity die casting. These runners have the cross-sectional area according to eq. 6:
Eq. 6:
n > 0.5 and m > 1.0 and A = cross sectional area in cm²In doing so, he obtains a slightly higher area reduction than with eq. 5 and avoids flow interruptions at the inlet wall of the sprue channel during pouring which would occur if friction losses were not taken into account. Nielsen summarizes the term 0.0226 · m · V to C, the equation (eq. 7) for determining the Nielsen standard inlet areas then being:
Eq. 7:
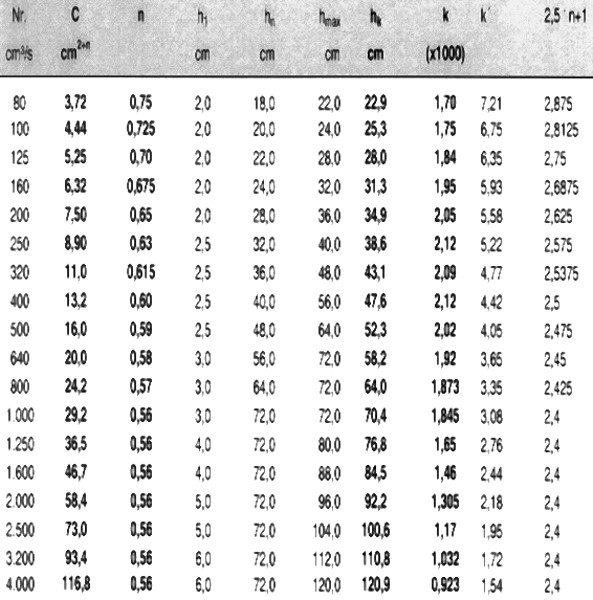
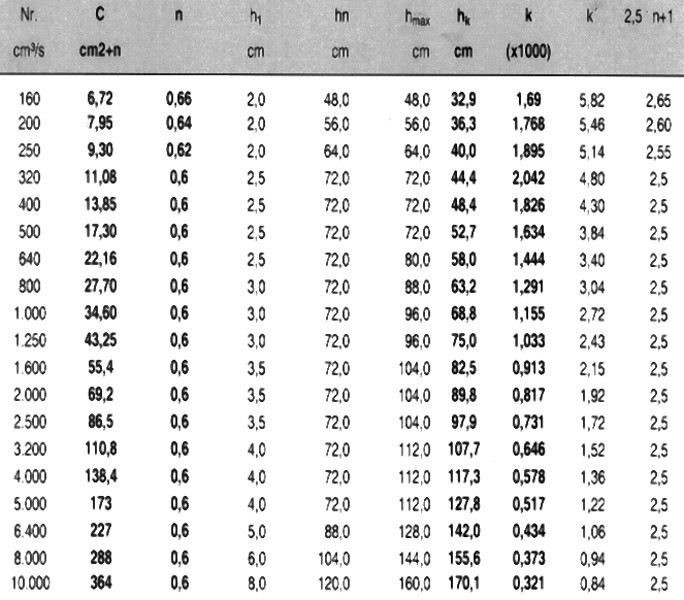
He also created tables for three standard runner types
- SI, cast iron and steel;
- SII, non-ferrous cast metal
- K1/3, gravity die casting and sand casting with a vertical parting plane
(Tables 1, 2 and 3) containing the relevant values of C and n for each runner size. The descriptions in the table are explained below:
Explanation of descriptions:
Nr. → corresponds to the nominal flow volume VN in cm³/s
C → constant of the cross-sectional area equation A=C/hn (eq. 7)
n → exponent attributed to the heads
hN → inlet length (head) at which the theoretical flow quantity would be VN
without taking friction into account.
hmax → greatest inlet head up to which the individual tables have been calculated
k → coefficient in the equation for the frictional resistance in the inlets up to the length h
if the quantity VN were to actually flow: RN = k · h2.5·n-1
2.5 · n - 1 → exponent in the equation for frictional resistance
Literature references:
Friedrich Nielsen, Gieß- und Anschnitttechnik - Grundlagen und Anwendung einer Methode, Giesserei-Verlag GmbH Düsseldorf, 1979.